

2.モード座標系の威力 (モード座標系と物理座標系)
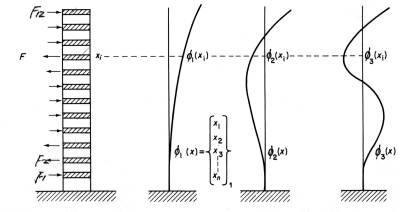
Fig.2-1における横荷重を受ける高層ビルの強制振動の運動方程式は、物理座標系を用いたマトリックス形式で(2-1)のように書ける。
Fig.2-1
Building displacement represented by normal modes.
Fig.2-1の12階建てのビルの場合、系は、12自由度で質量マトリックス:M
、減衰マトリックス:C、剛性マトリックス:K は、それぞれに(12×12)の大きさを、強制力F、加速度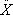 、速度
、速度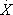 、変位X の各マトリックスは(12×1)の大きさを持ち、系は12個の固有値、ωr
、r=1〜12と12個の個有値ベクトルΦr(xi)、r =1〜12、i =1〜12を持つ。
、変位X の各マトリックスは(12×1)の大きさを持ち、系は12個の固有値、ωr
、r=1〜12と12個の個有値ベクトルΦr(xi)、r =1〜12、i =1〜12を持つ。
ここで固有値ベクトルを(2-2)のように並べた物がモードマトリックス(Modal Matrix)上である。
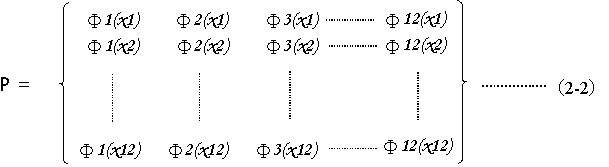
ここで、励振力が低周波域に集中している場合には、高周波の振動は励振されないので低次の周波数のモードΦ1(xi)、Φ2(xi)、Φ3(xi)だけが励振されると仮定できる。 また、i番目の変位xiはこれらの和として(2-3)で表され、
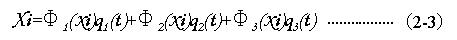
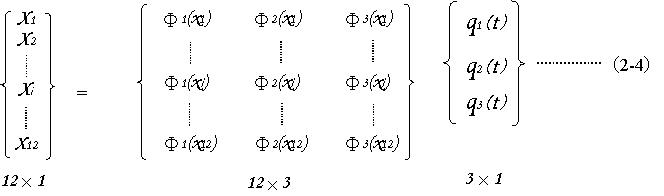
(2-2)を用いると(2-4)から(2-5)を得る。
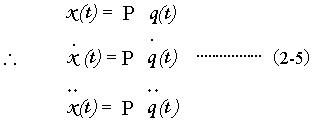
ここで(2-5)を(2-1)に代入し
P
の転置マトリックスPTをマトリックス
M
、C、
K に前から掛けると(2-6)を得る。
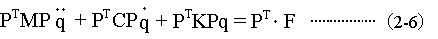
ここで、PTM
Pから1,2,3次の振動モードに対応する3個のモード質量
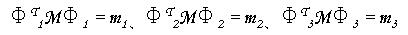
が得られる。
同様にPTCP、PTKPから3個のモード減衰係数と3個のモード剛性k1,2,3が求められ、(2-6)は、Fig.2-1に示されたΦ1
(x)、Φ2
(x)、Φ3
(x)の3個の振動モードに対応した1自由度系の強制振動の式になる。
すなわち、物理座標系では12自由度の振動系が、モード座標系Φでは3自由度系に縮小されることに気づく。
この方法は、モード合成法(Mode
Summation Method)として知られている解法で、複雑な構造物、一例として50階建てのビルにも適用できる。
実験モード解析から
ωγとΦγ(x)
、x=1,2・・・n
が正確に同定出来れば、(2-5)、(2-6)を用いて、複雑な系の振動がごく簡単に計算できる。これがモード座標系の威力である。
追補:
(1) PTMPとPTKPは通常対角マトリックスであるが、PTCPは対角にならないので、(2-6)は、連成項を持つ、この場合の解析については下記参考文献を参照されたい。
(2) Cが比例減衰:C=αM+βKとおける場合の解析も同文献を参照されたい。
参考文献:
(1) W.T.Thomson
Theory
of Vibration with Applications: 2nd Edition Prentice Hall. 1981
(2) 長松
昭男
![]()

![]()

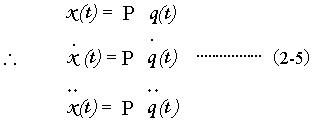
![]()
![]()